parsers
so, one of the main pieces of learning compilers is learning about parsers and their engineering.
what is a parser for? it is to see if for a stream of words can be derived given a set of rules. orr... if you prefer a formal defintion.
For a stream of words s and a grammar G, the parser builds a constructive proof that s can be derived in G
there are two ways to approach this problem. top down and bottom up (obviously)
in top down, we are starting from a given set of grammar and match the input stream against the productions of the grammar by predicting the next word. and in bottom up, we are starting with the tokens and accumulate context until the derivation is apparent.
what are context free grammars?
to formally understand parsers, we need to understand what context-free grammars (CFG) are.
a CFG is a set of rules or productions that describe how to form sentences.
the collection of sentences that derive from G is the language denoted L(G)
the benefit of using CFGs over Regular Experessions (RE) is that they are really well defined. take for instance, parantheses matching. REALLY HARD to do using REs but CFG super easy.
here is an example, the CGF is this
Expr -> ( Expr )
| Expr Op Expr
| name (or just something atomic)
Op -> x
÷
-
+
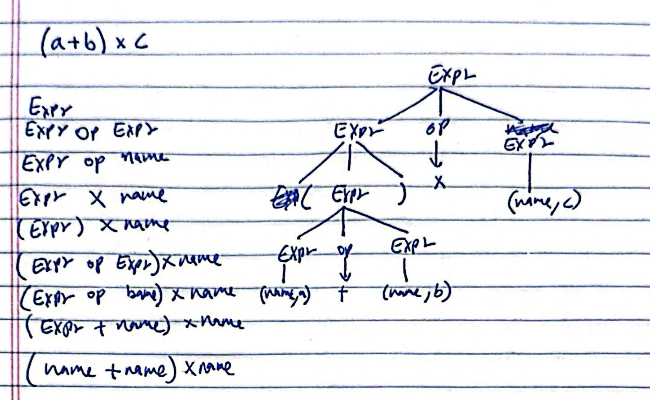
however there is ambiguity in this grammar if we tried to derive a + b * c. it wouldn't follow our algebraic rules of precedence and hence losing the entire meaning behind CFGs. good news is its fixable with a new grammar that includes a way to define precedence
Expr -> Expr + Term
| Expr - Term
| Term*
Term -> Term x factor
| Term ÷ factor
| Factor
Factor -> ( Expr )
| num
| name
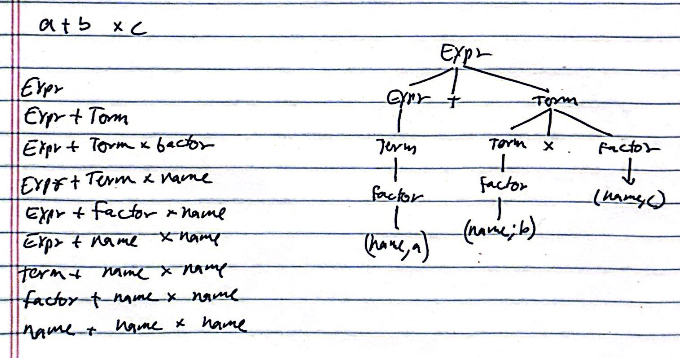
for precedence we can add more grammar from programming languages with say array subscripts or type casts which falls in the middle with arithmetic operations on the lower precedence and parantheses/subscript on the higher precedence
top down parsing
the efficiency of top down parsing depends on its ability to pick the correct production each time that it expands a non terminal element. the cost of choosing a wrong production is asymptotically equal to the size of the tree because it has to traverse all the way back and try unfolding with a new production now if the previous one was wrong (This is VERY BAD! its like refilling in all the bubbles on a scantron after finding out you missed question 2)
there is a whole section of why not to use left recursion and use right recursion but it is pretty intuitive if you thinks about it. but i will explain later cuz not really important
backtrack-free parsing
this means we need to now implement an algorithm that can mechanically determine, in one step, either the correct expansion or that the correct expansion does not exist in a sense implement oracular choice
we need to introduce the concept of lookahead which is looking at the next input token to choose the correct rule before trying to parse. this is called LL(1) parsing
L := left to right scan
L := leftmost derivation
1 := 1 token of lookahead
the foundation of this predictive parsing is two things called the FIRST and the FOLLOW sets which as the name suggests are explanatory. the FIRST is a set of terminals that can appear at the start of some string derived from X and the FOLLOW is the ones that can immediately appear after A in some derivation